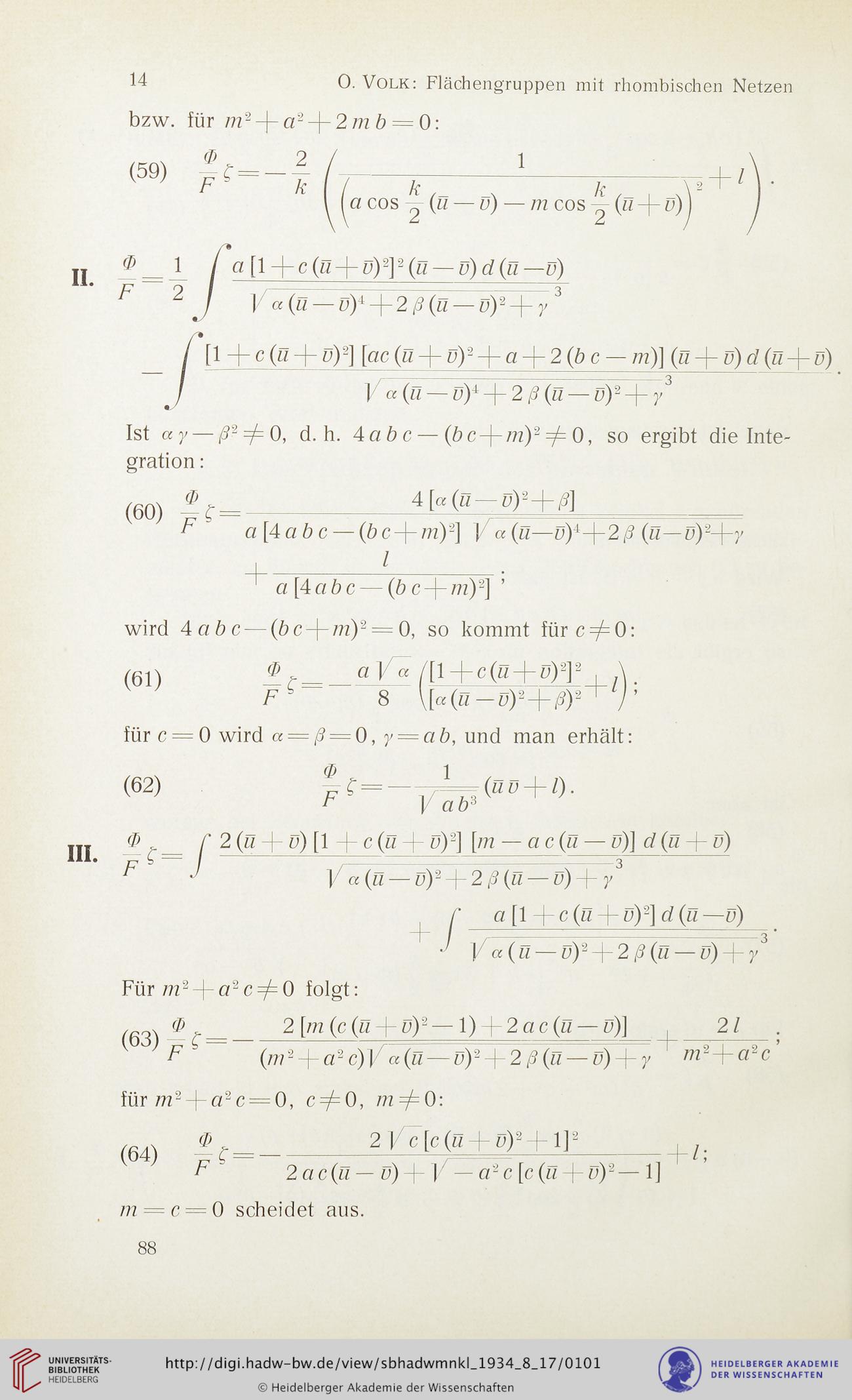DOI Seite / Zitierlink:
https://doi.org/10.11588/diglit.43680#0101
14
g [ 1 —c (zz —zz)2]2 (u — zz) d (zz —zz)
4 [« (zz — ZZ)2-H]
(60)
wird
(61)
(62)
]/ a(u — zz)4 -|- 2 /? (Z7 — zz)2 -p7 3
“FT + ■
— 772 COS — (ZZ-j—^) ) /
0
in.
0. Volk: Flächengruppen mit rhombischen Netzen
bzw. für 7722 —|—2 —2 772 ö = 0 :
x <7> 2
O9) =
0 1 /
II. -= - /
F 2
f*[1 —c (n —zz)2] [ac (zz —|— U)2 —|— <7 —|— 2 (6 c — 772)] (zz 4~ zz) <7 (zz 4 zz)
ZZ | a /[l+c(zz + zz)2]2 . \
l[«(Zz-zz)2+/?)2^7’
]/ ab3
r 2 (zz + zz) [1 + c (zz zz)2] [m — ac(ü — zz)] cl(ü.^-F)
] a (ZZ — ZZ)4 -\~2 ß(ll — ZZ)2 4- y3
Ist ay — 4 4=0, d. h. 4abc— (bc-\-m)2=/=0, so ergibt die Inte-
gration :
4_
F a [4a b c — (bc-\-m)2] |/«(zz—zz)4—2(z,z—zz)2—7'
, l
ci[4cibc — (bc-\-m)2]’
4cibc — (öc-|-77z)2 = 0, so kommt für c 4=0:
-f=-
Fs 8
für c — 0 wird a = ß = Q, y = ab, und man erhält:
F ^ = — ^7=
]/ a (zz — zz)2 -\-2 ß (zz — zz) 4 y
/’ ci [1 +c(z7 + ö)2] d(ü—V)
■ ]/ a(z7— Zz)2 + 2/?(zZ—zz) + y3
(a cos (zz — zz)
,L ,t( L//J 21
(63) - £ = - (w?2 + a2c)1/-a^_^2 + 2/?(s_^q^; + tF+ a2c’
Für m2-\-a2c=/=Q folgt:
$ 2 [772 (c (z7-]-zz)2— 1) 4~2« c (z7 — zz)]
F
für/722 -|-zz2c = O, 40, m=/=(F.
(64) -f= 2VT[c(a+p)2+!]2
f' 2ac(ü — o)+ T— a2r[c(n + o)2— 1]
722 ==c = O scheidet aus.
88
g [ 1 —c (zz —zz)2]2 (u — zz) d (zz —zz)
4 [« (zz — ZZ)2-H]
(60)
wird
(61)
(62)
]/ a(u — zz)4 -|- 2 /? (Z7 — zz)2 -p7 3
“FT + ■
— 772 COS — (ZZ-j—^) ) /
0
in.
0. Volk: Flächengruppen mit rhombischen Netzen
bzw. für 7722 —|—2 —2 772 ö = 0 :
x <7> 2
O9) =
0 1 /
II. -= - /
F 2
f*[1 —c (n —zz)2] [ac (zz —|— U)2 —|— <7 —|— 2 (6 c — 772)] (zz 4~ zz) <7 (zz 4 zz)
ZZ | a /[l+c(zz + zz)2]2 . \
l[«(Zz-zz)2+/?)2^7’
]/ ab3
r 2 (zz + zz) [1 + c (zz zz)2] [m — ac(ü — zz)] cl(ü.^-F)
] a (ZZ — ZZ)4 -\~2 ß(ll — ZZ)2 4- y3
Ist ay — 4 4=0, d. h. 4abc— (bc-\-m)2=/=0, so ergibt die Inte-
gration :
4_
F a [4a b c — (bc-\-m)2] |/«(zz—zz)4—2(z,z—zz)2—7'
, l
ci[4cibc — (bc-\-m)2]’
4cibc — (öc-|-77z)2 = 0, so kommt für c 4=0:
-f=-
Fs 8
für c — 0 wird a = ß = Q, y = ab, und man erhält:
F ^ = — ^7=
]/ a (zz — zz)2 -\-2 ß (zz — zz) 4 y
/’ ci [1 +c(z7 + ö)2] d(ü—V)
■ ]/ a(z7— Zz)2 + 2/?(zZ—zz) + y3
(a cos (zz — zz)
,L ,t( L//J 21
(63) - £ = - (w?2 + a2c)1/-a^_^2 + 2/?(s_^q^; + tF+ a2c’
Für m2-\-a2c=/=Q folgt:
$ 2 [772 (c (z7-]-zz)2— 1) 4~2« c (z7 — zz)]
F
für/722 -|-zz2c = O, 40, m=/=(F.
(64) -f= 2VT[c(a+p)2+!]2
f' 2ac(ü — o)+ T— a2r[c(n + o)2— 1]
722 ==c = O scheidet aus.
88